နေ့စဉ်ဘဝထဲက ရိုးရှင်းသော သင်္ချာများ

 

                                     နေ့စဉ်ဘဝထဲက ရိုးရှင်းသော သင်္ချာများ        

 

            မြန်မာစကားမှာ ပညာရှိတို့ တွေးကြည့်ရင် ပြေးကြည့်တာထက်မှန်တယ် ဆိုတဲ့ စကားရှိပါတယ်။ တကယ်လို့များ ပြေးကြည့်လို့ မရနိုင်တဲ့အခြေအနေမျိုးဆိုရင်ကော ဘယ်လိုဆိုကြပါမလဲ။ အဲ့ဒီလိုအခြေအနေမျိုးမှာ "ပညာရှိတို့ တွက်ကြည့်ရင် လက်ရှိမှာထက် မှန်တယ်" ဆိုချင်ပါတယ်။ တွေးတောဆင်ခြင်တွက်ဆတဲ့နည်းကို ကျွန်တော်တို့ဟာ ငယ်စဉ်ကလေးဘဝကတည်းက သင်္ချာစွမ်းရည်ကို အသုံးချရတဲ့ စကားနည်းတွေကစားရင်း ရင်းနှီးလာကြတာဖြစ်ပါတယ်။

 

တွက်ချက်ခြင်းဖြင့် ခန့်မှန်းခြင်း

            အရွယ်ရောက် ကြီးပြင်းလာတဲ့အချိန်မှာ ကလေးတစ်ရောက်ရဲ့အရပ်အမောင်း ဘယ်လောက်လာဖြစ်နိုင်မလဲဆိုတဲ့ ခန့်မှန်းချက် ကစားနည်းဟာ ပေါင်းနှုတ်မြှောက်စား သဘောတရားကို လက်တွေ့အသုံးချခဲ့ကြတဲ့ ကလေးဘဝ ကစားတစ်ခုဖြစ်ပါတယ်။ အရွယ်ရောက်ချိန်ရဲ့ အရပ်ကိုခန့်မှန်းတဲ့အခါ  အဖေအရပ်အမြင့် (လက်မ)နဲ့ အမေအရပ်အမြင့်(လက်မ)ကိုပေါင်း၊  ယောက်ကျားလေးအတွက်ဆို ၅ ထပ်ပေါင်း၊ မိန်းကလေးအတွက်ဆို ၅ နှုတ်၊ ရလာဒ်ကို ၂ နဲ့စားပြီး၊ ခန့်မှန်းခဲ့ကြတယ်မဟုတ်ပါလား။ သင်္ချာပုံစံနဲ့ ဖေါ်ပြရမယ်ဆိုရင်

for boy  = (father’s height+ mother’s height+ 5) / 2

for girl  = (father’s height+ mother’s height- 5) / 2

ဥပမာ ကလေးရဲ့ မိခင်က အရပ် ၅ ပေ ၂ လက်မ၊ ဖခင်က ၅ ပေ ၈ လက်မ ဆိုရင်

ယောက်ျားလေးဆိုရင်   ((၅x12 + 8)   + (5x12 + 2)  + 5)/2 = 5 ပေ 8 လက်မခန့်

မိန်းကလေးဆိုရင်         ((၅x12 + 8)   + (5x12 + 2)  - 5)/2 = 5 ပေ ၃ လက်မခန့်

            ရှိလာမယ်လို့ ခန့်မှန်းကြတာဖြစ်ပါတယ်။ ဒီလို ရိုးရှင်းတဲ့ သင်္ချာလုပ်ထုံးလေးကို အသုံးပြုပြီး ကလေးဘဝမှာကတည်းက နောင်အနာဂတ်ကို ခန့်မှန်းနိုင်တဲ့ စကားနည်းမျိုး ကစားနိုင်ခဲ့ကြတယ်ဆိုတာဟာ သင်္ချာပညာရပ်ရဲ့ အလှတရားတစ်ခုလို့ ဆိုနိုင်ပါတယ်။

            ဒါ့အပြင် ငါးမွေးကန်ထဲမှာ ငါးဘယ်နှစ်ကောင်လောက် ရှိနိုင်မလဲ ဆိုတဲ့ မေးခွန်းမျိုးဟာလည်း ပြေးကြည့်လို့ အဆင်မပြေနိုင်တဲ့ ကိစ္စမျိုးပါ။ အဲ့ဒီလိုအခြေအနေမျိုးမှာ နမူနာအဖြစ် ငါးကောင်ရေ ၃၀၀ ကို ဖမ်းပြီး အမှတ်အသားလုပ်မယ်။ အဲ့ဒီလို အမှတ်အသားလုပ်ထားပြီးသား ငါးအကောင် ၃၀၀ ကို ကန်ထဲကို ပြန်လွှတ်ပေးမယ်။ ပြီးတဲ့အခါမှာ အချိန်ကာကတစ်ခုခြားပြီး  အဲဒီကန်ထဲကပဲ နမူနာအဖြစ်  ငါးအကောင် ၃၀၀ ကို အသစ် ထပ်မံဖမ်းဆီးပါမယ်။ အဲ့ဒီ ထပ်မံဖမ်းဆီးလို့ ရတဲ့အထဲမှာ အမှတ်အသားလုပ်ထားတဲ့ အကောင် ဘယ်လောက်ပါသလဲဆိုတာကို အချိုးချကြည့်ပါတယ်။ တကယ်လို့ အဲ့ဒီလို ဒုတိယအကြိမ် နမူနာကောက်ယူတဲ့ ငါး အကောင် ၃၀၀ ထဲမှာ ၂၅ ကောင်က အရင်တုန်းက အမှတ်အသားလုပ်ထားတဲ့ ငါးတွေဆိုပါစို့။ အဲ့ဒီအခါမှာ အမှတ်အသားလုပ်ထားတဲ့ ငါးတွေရဲ့ အချိုးက 25 divided by 300, or 1/12 ဖြစ်ပါတယ်။

            စုစုပေါင်း အမှတ်အသားလုပ်ထားတဲ့ငါးက အကောင်သုံးရာ ရှိတာဖြစ်တဲ့အတွက်၊ အခြေခံ နမူနာကောက်ယူမှု အခြေခံစည်းမျဉ်း (basic sampling principle) အရ ခန်းမှန်းခြေပုံသေနည်းဟာ

 1/12 ~  300/N

ဖြစ်ပါတယ်။ အဲ့ဒီမှာ N က အဲ့ဒီ ငါးကန်ထဲမှာ ရှိနိုင်တဲ့ စုစုပေါင်းငါးအရေအတွက်ဖြစ်ပါတယ်။ ဒါကြောင့် နှစ်ဖက်စလုံးကို ၃၀၀ နဲ့စားပြီး ရှင်းလိုက်တဲ့အခါ N ~ 3,600 ဖြစ်ကြောင်း အကြမ်းဖျဉ်းခန့်မှန်းနိုင်ပါတယ်။ ဒီနည်းဟာ တောရိုင်းတရိစ္ဆာန် ထိမ်းသိမ်းစောင့်ရှောက်သူတွေ လက်တွေ့ သုံးတဲ့နည်းလမ်းပါ။

            ကျွန်တော်တို့ဟာ သိပ္ပံပညာရှင်ကြီးတွေဖြစ်လာကြစေဦးတော့၊ အဲဒီလိုရိုးရှင်းလွယ်ကူတဲ့ သင်္ချာတွေကို အသုံးချပြီး ကမ္ဘာကြီးရဲ့ အရွယ်အစား၊ စကြာဝဠာကြီးရဲ့အရွယ်အစား၊ စကြာဝဠာကြီးထဲက ကြယ်အရေအတွက်စုစုပေါင်း စတာတွေအထိ ခန့်မှန်းတွက်ချက်နိုင်ခဲ့ကြတယ်မဟုတ်ပါလား။

 

Magic squares နှင့် ပေါင်းခြင်း

            ကိန်းဂဏန်းတွေ ပေါင်းစပ်မှုနဲ့ ပတ်သက်ပြီး Magic squares ကစားနည်းတွေကို  2200 B.C လောက်ကတည်းက တရုတ်တို့ အိန္ဒိယ တို့မှာ ကစားခဲ့ကြတာပါ။ လေးတန်းလေးတိုင် (၁၆ ကွက်) ပါရင် fourth order, ငါးတန်းငါးတိုင် (၂၅ ကွက်) ပါရင် fifth order magic square ဖြစ်ပါတယ်။ အဲ့ဒီ magic square တွေရဲ့ ပေါင်းလာဒ်ဖြစ်ရမဲ့တန်ဘိုး S ဟာ order N အပေါ်မူတည်ပါတယ်။ အဲ့တာကို ပုံသေနည်း S = (N/2) (N² +1) နဲ့ တွက်ကြည့်နိုင်ပါတယ်။ ဥပမာ fifth order magic square မှာ ပါတဲ့ ကိန်းငါးခုရဲ့ အတန်းလိုက် ဒေါင်လိုက် ဒေါင့်ဖြတ်အလိုက် ပေါင်းခြင်း ရလာဒ်ဟာ [ S = (5/2) (5² + 1)] ၆၅ ဖြစ်ရပါမယ်။

            Magic squares ကစားနည်းတွေထဲက အလွယ်ဆုံးနဲ့ အငယ်ဆုံး Magic squares စကားနည်းက သုံးတန်းသုံးတိုင်ပါတဲ့ third order magic square ပါ။အလျားလိုက် ဒေါင်လိုက် ဒေါင့်ဖြတ် ပေါင်းခြင်း ၁၅ ရစေမဲ့ သုံးတန်းသုံးတိုင် magic square တစ်ခုကိုစကားမယ်ဆိုပါစို့။ ဒီလိုအချိန်မှာ ကျွန်တော်တို့ အသုံးချတဲ့သင်္ချာဟာ ပေါင်းခြင်းလုပ်ထုံးပဲဖြစ်ပါတယ်။ အဲ့ဒီ သုံးတန်းသုံးတိုင်ဂဏန်းပေါင်းပြဿနာကို ပြေလည်စေဖို့ ဖြစ်နိုင်ခြေရှိတဲ့ ကိန်းပေါင်းလာဒ်တွေဟာ အောက်ပါအတိုင်းဖြစ်ပါတယ်။

6+ 5+ 4 = 15,

7+ 5+ 3 = 15,

7+ 6+ 2 = 15,

8+ 4+ 3 = 15,

8+ 5+ 2 = 15,

8+ 6+ 1 = 15,

9+ 4+ 2 = 15,

9+ 5+ 1 = 15

            ဒီပေါင်းခြင်းကိန်းတွဲတွေကို ကြည့်ရှုဆင်ခြင်တဲ့အခါ ၅ ဟာ ဖြစ်နိုင်တဲ့ ပေါင်းခြင်း ၈ တွဲမှာ ၄ ကြိမ်အထိ၊ တခြားဂဏန်းတွေထက်ပိုပို ပါဝင်နေတယ်ဆိုတာ တွေ့ရပါတယ်။ ဒါကြောင့် ၅ ကို စကွဲရဲ့ အလယ်မှာ ထားသင့်တယ်လို့ တွေးနိုင်ပါတယ်။ အဲ့ဒီနောက် ၅ ပါဝင်တဲ့ ညီမျှခြင်း ၄ ကြောင်းကို စကွဲရဲ့ အလယ်တိုင်၊ အလယ်တန်း နဲ့ ဒေါင့်ဖြတ် ၂ နေရမှာ နေရာချလိုက်မယ်ဆိုရင် ပေါင်းခြင်း ၁၅ ရမဲ့ ကိန်းသုံးလုံးပါ စတုရန်းကွက် ကစားနည်းကို အောင်မြင်ပြီဖြစ်ပါတယ်။

            ဒီကစားနည်းမှာ ရိုးရှင်းတဲ့ ပေါင်းခြင်းကို အသုံးချသွားတယ်ဆိုပေမဲ့၊ တန်ဘိုးအချိုးကျပျံ့နှံ့ခြင်း(symmetrical / normal distribution) သဘောတရားတွေ နဲ့ ပျှမ်းမျှကိန်း၊ အလယ်ကိန်း၊ ကြိမ်နှုန်း ( mean, median, mode) သဘောတရားတွေပါ ပါဝင်ဖွဲ့စည်းထားတယ်ဆိုတာ တွေ့နိုင်မှာဖြစ်ပါတယ်။

 

ကိန်းစဉ်တန်းနှင့် အလောင်းအစားဥပဒေသ

            သင်္ချာဆိုတာ ပညာရှင်တွေမှသာ အကျိုးရှိရှိအသုံးချနိုင်တာမဟုတ်ပါဘူး။ ဘယ်လိုလူကမဆို လက်တွေ့အသုံးချနိုင်ပါတယ်။ သင်္ချာဟာ လူတန်းစားမခွဲခြားပါဘူး။  အလွန်ရိုးရှင်းတဲ့ ပေါင်းခြင်းကိန်းစဉ်တန်းလေးတခုကိုကြည့်ရှုဆင်ခြင်ပြီး လက်တွေ့ဘဝရဲ့ မထင်မှတ်တဲ့နေရာမှာ အသုံးချသွားတာတွေလည်းရှိပါတယ်။ ဥပမာအားဖြင့် ကျွန်တော်တို့ ငယ်စဉ်က ပေါင်းခြင်း၊ မြှောက်ခြင်း နဲ့ ထပ်ကိန်း သဘောတရားတွေကို ဆက်စပ် သင်ယူခဲ့ရတဲ့နေရာရှိပါတယ်။ အဲ့တာကတော့၊ တစ် ကိုယူ၊ အဲ့ဒီကိန်း တစ် နဲ့ပဲပြန်ပေါင်း၊ ရလာတဲ့ နှစ်ကို နှစ်နဲ့ပေါင်း၊ ရလာတဲ့ ၄ ကို ၄ နဲ့ပေါင်း၊ စသည်ဖြင့်  အဲ့ဒီလုပ်ငန်းစဉ်ကို ထပ်ကာ ထပ်ကာ ပြန်လုပ်တဲ့ ပေါင်းခြင်းမျိုးဖြစ်ပါတယ်။ အဲ့ဒီလိုလုပ်ဆောင်တဲ့အခါမှာ 1, 2, 4, 8, 16, 32, 64...   ဆိုတဲ့ "geometric progression" ရလာပါတယ်။ အဲ့ဒီ သင်္ချာသဘောတရားကို ပြင်ပ လက်တွေ့ကမ္ဘာမှာ အကျိုးရှိရှိအသုံးချသွားသူတွေရှိပါတယ်။ အဲ့ဒီ geometric progression သင်္ချာ ကိန်းစဉ်တန်းကိုကြည့်ပြီး "လောင်းကစားလုပ်တဲ့ နေရာမှာ တကြိမ်ထက် တစ်ကြိမ်၊  နှစ်ဆ နှစ်ဆ သာ တိုးပြီးလောင်းမယ်ဆိုရင်၊ ဘယ်သောအခါမှ မရှုံးနိုင်ဘူး" ဆိုတဲ့ အချက်ကို တွေ့ရှိခဲ့ကြတာဖြစ်ပါတယ်။ အကြောင်းကတော့၊ ၁ ကနေ  ၃၂ အထိ ပေါင်းခြင်းဟာ ၆၃ ဖြစ်ပြီး သူနဲ့ ကပ်လျက် နောက်တစ်ခုတန်ဖိုးက ၆၄ ဖြစ်တဲ့အတွက်၊ လောင်းကစားတဲ့အခါ မထမ ၆ ကြိမ် ဆက်တိုက် ရှုံးစေဦးတော့ ခုနှစ်ကြိမ်မြောက်မှာသာ နိုင်ခဲ့မယ်ဆိုရင် အရှုံးအားလုံးအတွက် ကာမိတဲ့အပြင် အမြတ်ပါရနိုင်တယ် ဆိုတဲ့ အချက်ကို ဖော်ထုတ်အသုံးချခဲ့ကြတာဖြစ်ပါတယ်။

 

ပိုက်သာဂိုရပ်စ် သီအိုရမ်နှင့် သုံးဖက်တိုင်း အကွာအဝေး

            ဆိုပါစို့ ကျွန်တော်တို့ဟာ ခရီးထွက်တဲ့အခါ မဖြစ်မနေ ထီးတစ်ချောင်းပါအောင်သယ်ရမယ်။ ထီးကလည်း ခေါက်ထီးမဟုတ်ဘူး ချာလီထီး။ ခရီးဆောင်အိတ်ထဲမှာ ချာလီထီးကို အိတ်အောက်ခြေအစွန်းနဲ့ အိတ်ထိပ်စွန်းအတိုင်း ထောင့်ဖြတ်ထားပြီး ထီးကိုထည့်မယ်ဆိုရင် အဲ့ဒီထီးဟာ အရှည်ဆုံး ဘယ်လောက်အထိ ဖြစ်လို့ရလဲ ဆိုတဲ့ အခြေအနေမျိုး ကြုံလာပြီဆိုပါစို့။ လွယ်အောင် ပြောရရင်တော့ ပုံမှာ ပြထားတဲ့အတိုင်း AF ရဲ့ အလျားကို ရှာဖို့ လိုအပ်လာပြီဆိုပါစို့။

            အဲ့လိုအခြေအနေမှာ ခရီးဆောင်အိတ်ရဲ့အတိုင်းအတာတွေကို သိထားရင် ပြေးကြည့်နေစရာမလိုပါဘူး။ လွယ်လွယ်ကူကူ တွက်ကြည့်လိုက်ရုံပါပဲ။ သဘောတရားကလည်း ကျွန်တော်တို့နဲ့ ရင်းနှီးပြီးသား ပိုက်သာဂိုရပ်စ် သီအိုရမ်ကို ချဲ့ထွင် အသုံးချသွားတာသာ ဖြစ်ပါတယ်။ ပိုက်သာဂိုရပ်စ် သီအိုရမ်အရ

တဖန်

နောက်ဆုံး အလွယ်တကူ အနှစ်ချုပ်လိုက်ရင်

AB ² + BC ² + FC ² = AF ²

6 ² + 2 ² + 3 ² = AF²

36 + 4 + 9 = AF²

            ဖြစ်ပြီး ထုထည်ရှိတဲ့ အရာဝတ္ထုတစ်ခုရဲ့ အတိုင်းအတာတွေကို သိမယ်ဆိုရင်၊ အဲ့ဒီအရာဝတ္ထုရဲ့ အောက်ခြေထောင့်နဲ့ ထိပ်ထောင့် နှစ်ခုရဲ့ ထောင့်ဖြတ်အကွာအဝေးကို နှစ်ဖက်တိုင်းမှာအသုံးချတဲ့ ပိုက်သာဂိုရပ်စ်သီအိုရမ်သဘောတရားကိုအသုံးချပြီး သုံးဖက်တိုင်းအတွက် တိုးချဲ့အသုံးပြုနိုင်တယ်လို့ ကောက်ချက်ဆွဲနိုင်ပါတယ်။

 

အရွယ် အကျယ် ထုထည် အလေး                   

            လက်တွေ့ပြင်ပလောကမှာ အများဆုံးတွေ့ရတဲ့ ထပ်ကိန်းတွေက နှစ်ထပ် နဲ့ သုံးထပ် ဖြစ်ပါတယ်။  အင်္ဂလိပ်လို နှစ်ထပ်ကို စကွဲ လို့  square ခေါ်ရတဲ့အကြောင်းက L meter အလျားရှိတဲ့ စတုရန်းတစ်ခုရဲ့ ဧရိယာ A  ဟာ L x L တနည်း  L²  (L Square) ဖြစ်တဲ့အတွက်ကြောင့်ပါ။ အလားတူပဲ အနားတစ်ဖက်ရဲ့အလျား L ရှိတဲ့ အံစာတုံး (cube) တစ်ခုရဲ့ ထုထည်ဟာ L cube ဖြစ်ပါတယ်။ အခြားပုံသဏ္ဌာန်တွေအတွက်လည်း စက်ဝိုင်းရဲ့ ဧရိယာဆိုရင်     square ဖြစ်ပြီး၊ စက်လုံးရဲ့ ထုထည်ဆိုရင်   cube ဖြစ်ပါတယ်။  ဒါကြောင့် အရာဝတ္ထုတစ်ခုရဲ့ ဧရိယာဟာ သူ့ရဲ့အခြေခံအရွယ်အစားရဲ့ အတိုင်းအတာနှစ်ထပ်နဲ့ တိုက်ရိုက်အချိုးကျတယ်လို့ ကောက်ချက်ပြုနိုင်ပြီး၊ ထုထည်က အခြေခံအရွယ်အစား အတိုင်းအတာသုံးထပ်နဲ့ တိုက်ရိုက်အချိုးကျတယ်လို့ ပြောနိုင်ပါတယ်။ အဲ့ဒီအချက်ဟာ သာမန်လို့ ထင်ရပေမဲ့ လက်တွေ့ပြင်ပကမ္ဘာရဲ့ ရုပ်လောက ဆက်စပ်မှုတွေကို စဉ်းစားတွေးခေါ်တဲ့အပေါ်မှာ အများကြီး အကျိုးသက်ရောက်မှု ရှိပါတယ်။

            ဥပမာအားဖြင့်  ပုံစံတူ ခွေးနှစ်ကောင် မှာ တစ်ကောင်က တခြားတစ်ကောင်ထက် အရွယ်အစား(အရပ်)က နှစ်ဆမြင့်တယ်ဆိုရင်၊ အဲ့ဒီလို ပိုကြီးတဲ့ခွေးရဲ့ အလေးချိန်ဟာ ငယ်တဲ့ခွေးအလေးချိန်ရဲ့ နှစ်ဆမဟုတ်ပါဘူး။ အလေးချိန်ဟာ ထုထည်နဲ့ဆက်စပ်တဲ့အတွက် ထုထည်ဟာ အရွယ်အစားရဲ့   သုံးထပ်နဲ့ အချိုးညီတယ်ဆိုတဲ့ သဘောတရားရှိပြီးဖြစ်ရှိတဲ့အတွက်  (2³ = 8) ၈-ဆ ပိုလေးမှာဖြစ်ပါတယ်။

            တခါဆက်ပြီး စဉ်းစားမယ်ဆိုရင် ကြီးတဲ့ခွေးက ငယ်တဲ့ခွေးအလေးချိန်ရဲ့ ၈-ဆ လေးပေမဲ့   သူ့ရဲ့အရိုးတွေကတော့ ရှစ်ဆ ပိုပြီး သန်မာမှာ ကြီးမားမှာ မဟုတ်ပါဘူး။ အကြောင်းကတော့ အရိုးရဲ့ သန်မာမှုဟာ  အရိုးတစ်ရိုးရဲ့   ထိတ်ဖြတ် ဧရိယာ (cross-sectional area) နဲ့ အချိုးညီတဲ့အတွက် ကြီးတဲ့ခွေးရဲ့ အရိုးအရွယ်အစားက ငယ်တဲ့ခွေး အရိုးအရွယ်အစားရဲ့ (၂^၂) လေးဆပဲဖြစ်ပါမယ်။ ခွေးကြီးရဲ့ အရိုးအရွယ်အစား တနည်း အရိုးသန်မာမှုက ခွေးငယ်ရဲ့ ရှစ်ဆ ဖြစ်စေချင်ရင် ခွေးကြီးရဲ့ အရိုးထိပ်ဖြတ်ဧရိယာဟာ ခွေးငယ်ထက် square root of 8 (2.83) ဆ ဖြစ်ရမှာပါ။

            အဲ့ဒီသဘောတရားကို အသုံးပြုပြီး ဆင်တွေနဲ့ ပတ်သက်တဲ့ အချက်ကို ဆင့်ပွားကောက်ချက် ဆွဲကြည့်နိုင်ပါတယ်။ ဆင်တစ်ကောင်ဟာ ကြီးပါတယ်ဆိုတဲ့ ခွေးတစ်ကောင် အရွယ်အစားရဲ့ ၁၀ ဆ ဆိုရင်၊ ဆင်ရဲ့အလေးချိန်ဟာ  ခွေးအလေးချိန်ရဲ့  (၁၀ ³) အဆတစ်ထောင်ဖြစ်ပါတယ်။ ဆင်ရဲ့ ကိုယ်ခန္တာအလေးချိန်ကိုထမ်းဆောင်နိုင်မဲ့ ခြေထောက်တွေဟာ  ယခုပြဿနာမှာ နှိုင်းယှဉ်နေတဲ့ ခွေးရဲ့ခြေထောက်အရွယ်အစားရဲ့ square root of 1000 (31.62) ဆ ဖြစ်ရပါမယ်။ ဒါကြောင့် ဆင်ဟာ ခွေးအရပ်ရဲ့ ၁၀ ဆ ဖြစ်မယ်ဆိုရင်၊ ဆင်ရဲ့ ခြေထောက်ဟာ ခွေးခြေထောက် အရွယ်အစားရဲ့ ၃၂ ဆ ခန့် ရှိရမှာဖြစ်တယ်လို့ ယေဘုယျ ကောက်ချက်ဆွဲနိုင်ပါတယ်။

            ဒါ့အပြင် ဒီ ဧရိယာ ထုထည် သဘောတရားအဆက်အစပ်ဟာ လူ့အသက်ကယ်တဲ့နေရာ ဆေးပညာမှာလည်း ရှိနေပါတယ်။ လူတစ်ရောက်အတွက်လိုအပ်တဲ့ ဆေးဝါးပမာဏကို တွက်ချက်တဲ့အခါ များသောအားဖြင့် ကိုယ်အလေးချိန်အပေါ် မူတည်ပြီး စဉ်းစားလေ့ရှိပါတယ်။ ဒါပေမဲ့ အေအိုင်ဒီအက်စ်၊ ကင်ဆာ၊ အသည်းရောဂါ ဘီ အမျိုးအစား နဲ့ တစ်ချို့သောအခြားရောဂါတွေကို ကုသရာမှာတော့ ခန္ဒာကိုယ်အလေးချိန်ထက်၊ ခန္ဒာကိုယ်မျက်နှာပြင်ဧရိယာ (Body Surface Area) ကို အသုံးပြုလေ့ရှိပါတယ်။ အဲ့ဒီ BSA ကို ရှာတဲ့အခါမှာ သုံးတဲ့ " The DuBois formula" ဟာ

BSA = 0.007184 Wt ^0.425 Ht ^0.725

Wt = weight in kilograms, and

Ht = height in centimeters

            ဖြစ်ပါတယ်။ ဒီပုံသေနည်းဟာ စက်လုံးတို့ ထုချွန်တို့အတွက် ထုထည်ကို သူ့ရဲ့အတိုင်းအတာတွေပေါ်မူတည်ပြီး ရှာတဲ့ ဂျီဩမေထြီရဲ့ အ‌ခြေခံပုံသေနည်း တွေနဲ့ ခပ်ဆင်ဆင်ဖြစ်ပါတယ်။ ဆင်သာဆင်ပြီး မတူညီရတဲ့အကြောင်းက လူဟာ မတူညီတဲ့ ဂျီဩမေထြီပုံစံအမျိုမျိုးနဲ့ ပေါင်းစပ်ဖွဲ့စည်းထားတာကြောင့်ပါ။ သတ္ထုချရမယ်ဆိုရင် သင်္ချာပညာ အခြေခံလုပ်ထုံးလေးတွေဖြစ်စေဦးတော့ လူ့လောကသဘာဝကြီးရဲ့ လက်တွေ့ဖြစ်စဉ်တွေမှာ တွေးတော တွက်ဆ အသုံးချနိုင်တယ် ဆိုတဲ့အချက်ပဲဖြစ်ပါတယ်။

 

ဘဝကစားပွဲများနှင့် စုပေါင်းအကျိုးအမြတ်(Utility)

            ငွေတစ်သန်းဆုကြေးပေးမဲ့ ရုပ်သံဖျော်ဖြေရေးအစီအစဉ်တစ်ခုမှာ ပြိုင်ပွဲဝင်တစ်ဉီးဟာ မေးခွန်းတွေကို မှန်ကန်အောင်ဖြေဆိုနိုင်ခဲ့တဲ့အတွက် ဆုငွေ ၇၅,၀၀၀ ရရှိနေပြီဆိုပါစို့။ အဲ့ဒီလိုအချိန်မှာ နောက်ထပ်မေးခွန်းတစ်ခုကို ထပ်ပြီးဖြေဆိုရမှာဖြစ်ပါတယ်။ သူဟာ အဖြေကို သေသေချာချာ ပိုင်ပိုင်နိုင်နိုင် မသိပါဘူး။ အမှန်တော့ ပေးထားတဲ့မေးခွန်း လေးခုထဲက တစ်ခုကို ရွေးရမှာဖြစ်ပါတယ်။ တကယ်လို့ ရွေးတဲ့အဖြေ မှားရင် ရထားတဲ့ ငွေ ၇၅,၀၀၀ ထဲက ၂၅,၀၀၀ အနှုတ်ခံရမယ်၊ သူ့အတွက် ဆုငွေ ၅၀,၀၀၀ ပဲကျန်မယ်။ တကယ်လို့ သူ့အဖြေက မှန်တယ်ဆိုရင်တော့ ဆုငွေဟာ ၁၅၀,၀၀၀ ဖြစ်လာပါမယ်။ ဒါ့အပြင် တစ်သန်းရနိုင်မဲ့ အခွင့်အရေးလည်း ဆက်ရှိနေမယ်။ အဲ့ဒီအခြေအနေမျိုးမှာ သူဟာ လက်ရှိရထားတဲ့ ၇၅,၀၀၀ ကိုယူပြီး ပြိုင်ပွဲက ထွက်လိုက်ရမလား။ ဒါမှမဟုတ် သူဟာ အဲ့ဒီ ဂိမ်းကို ဆက်ကစားမလား၊ မေးခွန်းကို ဖြေလိုက်ရမလား ဆိုတာ ဆုံးဖြတ်ရပါမယ်။ အဲ့ဒီလို ဆုံးဖြတ်နိုင်ဖို့အတွက် Utility သဘောတရားကို အသုံးချပါမယ်။

Fig. A typical Utility curve

 

 

y = K√x, K > 0. ဆိုတဲ့ Utility သတ်မှတ်ချက်အရ

ဆုံးရှုံးနိုင်တဲ့စုပေါင်းပမာဏ က = K √25,000 = 158.1 K  ဖြစ်ပြီး၊

တကယ်လို့ သူ့အဖြေမှန်နိုင်ခြေက p  ဖြစ်မယ်ဆိုရင်

သူ့ရဲ့ ရရှိနိုင်တဲ့ စုပေါင်းပမာဏ = p K √100,000 = 316.2 K p ဖြစ်ပါတယ်။

            အဲ့တာကြောင့် ကောက်ချက်ဆွဲနိုင်တာက၊ သူရနိုင်တဲ့စုပေါင်းပမာဏ ဟာ သူဆုံးရှုံးနိုင်တဲ့ စုပေါင်းပမာဏထက် ကြီးရင်၊ သင်္ချာနည်းနဲ့ ပြောရင်

316.2 K p >  158.1 K က true ဖြစ်မယ်ဆိုရင်၊ ဂိမ်းကို ဆက်ကစားသင့်တယ် လို့ ပြောနိုင်ပါတယ်။             ကိန်းဂဏန်းအရပြောရရင် သူ့ရဲ့အဖြေမှန်နိုင်ခြေ p ဟာ 50% ကျော်မယ်ဆိုရင် ဆက်ကစားသင့်တယ်လို့ ဆိုလိုတာပါ။ ပေးထားတဲ့ အဖြေလေးခုထဲက ၂ ခုဟာ သေချာပေါက်မှားတယ်လို့သိထားရင် ကျန်တဲ့ အဖြေနှစ်ခုထဲက တစ်ခုကို ရွေးရမှာဖြစ်တဲ့အတွက် သူ့ရဲ့အဖြေမှန်နိုင်ခြေက 50% ရှိတဲ့အတွက်၊ အဲ့ဒီလိုအခြေအနေမျိုးမှာ မဖြစ်မနေ ဆက်ကစားသင့်တယ်လို့ ဆုံးဖြတ်သင့်ပါတယ်။

            ဒါ့အပြင် အရေးအကြီးဆုံးအချက်က တကယ့်တကယ် စုပေါင်းအကျိုးအမြတ်တွက်တဲ့အခါမှာ၊ တကယ်လို့ သူဆက်ကစားရင် "သန်းဆုရှင်" ဖြစ်နိုင်တယ်ဆိုတဲ့ အနာဂတ်အကျိုးအမြတ်နဲ့၊ တကယ်လို့ ဒီတကြိမ် အဖြေမှားခဲ့ရင်တောင် သူ့မှာ ဆက်ကစားခွင့်ရှိနေသေးတဲ့အတွက် နောက်ထပ်မေးခွန်းတွေမှာ မှန်အောင်ဖြေနိုင်ခဲ့ရင် အခုတစ်ကြိမ်မှာ သူ ဆုံးရှုံးခဲ့တဲ့ ၂၅,၀၀၀ ကိုပါ ပြန်ရနိုင်ချေရှိသေးတာတွေကိုပါ ထည့်တွက်ရင်၊ စုပေါင်းအကျိုးအမြတ်အဖြေဟာ 316.2 K p ထက်ပိုမိုကြီးမားလာနိုင်တယ်။ အဲ့ဒီလို အခြေအနေမျိုးမှာ သူ့ရဲ့အဖြေမှန်နိုင်ခြေဟာ ၅၀% အောက် နည်းစေဉီးတော့၊ သူ့ရဲ့အဖြေရွေးချယ်မှုမှန်နိုင်ခြေဟာ အနဲဆုံး ၂၅% ရှိနေတဲ့အတွက်၊ ဂိမ်းကို ဆက်ကစားသင့်တယ်လို့ သင်္ချာတွက်ချက်မှုနဲ့ ကိန်းဂဏန်းတွေက တိုက်တွန်းနေပါတယ်။

 

အလင်းအမှောင် အပြင်းအပျော့

                                 အသံတို့ အလင်းတို့ဟာ သူတို့ရဲ့ မူလရင်းမြစ်ထွက်ပေါ်ရာနေရာကနေ ဝေးသွားမယ်ဆိုရင် လျှင်မြန်တဲ့နှုန်းနဲ့ အားပျော့သွားပါတယ်။ ဆူညံသံကနေ နဲနဲ ခွာလိုက်ရင် နားခံသာတဲ့အဆင့်၊ ပိုလှမ်းအောင်ခွာလိုက်ရင် တိုးသွားတဲ့အဆင့်၊ နောက်ဆုံး အကွာအဝေးအတိုင်းအတာတစ်ခုမှာ အသံဟာ ပျောက်သွားမှာပါ။ အဲ့ဒီလိုပဲ လက်နှိပ်ဓါတ်မီးရဲ့အလင်းရောင်ဟာ အနီးအနားမှာဆိုရင် ထင်ရှားတောက်ပသလောက် အဝေးကိုလှမ်းပြီးထိုးရင် ကွယ်ပြောက်လုနီးနီးထိ ဖြစ်သွားပါတယ်။ ဒီအဖြစ်အပျက် သဘောတရားကို သင်္ချာရဲ့ ပြောင်းပြန် နှစ်ထပ် (inverse square)သဘောတရားက ကောင်းကောင်းရှင်းပြနိုင်ပါတယ်။ inverse square function တစ်ခုအတွက် အခြေခံ စံပုံသေနည်းက

y = k/x2 , where k is a constant of proportionality

ဖြစ်ပါတယ်။

 

                                                            ဥပမာ ၄၀ ဝပ်မီးသီးတစ်လုံးရဲ့ ၁ စကွဲမီတာပေါ်မှာ ကျရောက်မဲ့ အလင်းစွမ်းအား (L) ဟာ  40 Watts/4 pi r² ဖြစ်မယ်ဆိုရင်၊ တကယ်လို့ ကျွန်တော်တို့ဟာ အဲ့ဒီမီးသီးကနေ ၂ မီတာဝေးသွားမယ်ဆိုရင် အလင်းဟာ 4 Square Meter အပေါ်မှာ သက်ရောက်ပေးရမှာဖြစ်ပြီး၊ ၃ မီတာဝေးကွာသွားပြီဆိုရင် မီးသီးရဲ့အလင်းဟာ ဧရိယာ 9 Square Meter အပေါ်မှာ ပျံ့နှံ့ကျရောက်ပေးရမှာဖြစ်ပါတယ်။ ဒါကြောင့် အလင်းအားဟာ အကွာအဝေးနှစ်ထပ်နဲ့ ပြောင်းပြန်အချိုးကျနေကြောင့် ဝေးကွာသွားလေလေ အလင်းအသက်ရောက်မှုက မြန်မြန်ဆန်ဆန် လျော့နည်းသွားလေဖြစ်ရတာပါ။ ရူပဗေဒ မှာရှိတဲ့ အလင်းပြင်းအား ပုံသေနည်းဟာ E = I/r² ဖြစ်တဲ့အတွက် ဒါဟာ inverse square law ကို တိုက်ရိုက်ပုံဖေါ်ထားတယ်လို့ ပြောနိုင်ပါတယ်။ ဒီသဘောတရားကို ထပ်မံချဲ့ထွင် ဆင်ခြင်ပြီး နေမိသားစုထဲက ဘယ်ဂြိုဟ်မှာ လူတွေအသက်ရှင်နေထိုင်လို့ ရနိုင်လောက်မလဲဆိုတာကို အလင်းရောင် ရရှိမှု ရှုဒေါင့်က ကြည့်ပါစို့။

            ရာသီဥတုသာယာတဲ့ နွေရာသီ နေမွန်းတည့်ချိန်မှာ ကျွန်တော်တို့နေထိုင်ရာအရပ်မှာ ရတဲ့ နေရဲ့အလင်းရောင် ပမာဏကို ဆင်ခြင်ကြည့်ပါ။ ကျွန်တော်တို့ကမ္ဘာကနေတွက်ရင် နေနဲ့ တစ်ဆခွဲပိုဝေးတဲ့ အင်္ဂါဂြိုဟ်ပေါ်မှာဆို နေရဲ့အလင်းအားဟာ L/1.5² သို့မဟုတ် အခု ကျွန်တော်တို့ကမ္ဘာမှာ လင်းနေတဲ့အလင်းရဲ့ ၄၄% လောက်ရှိမယ်လို့ တွက်ဆဆင်ခြင်လို့ရပါတယ်။ ယေဘုယျပြောမယ်ဆိုရင် အဲ့ဒီအလင်းရောင် ပမာဏဟာ လူသားတွေ အသက်ရှင်သန်နိုင်ဖို့ လုံလောက်ပါတယ်။ တကယ်လို့ ကမ္ဘာနဲ့ယှဉ်လိုက်ရင် နေကနေ အဆသုံးဆယ် ပိုဝေးတဲ့ နက်ပကျွန်းဂြိုလ်ပေါ်မှာ ရှိနိုင်တဲ့ နေရဲ့အလင်းဟာ L/30² ဖြစ်တဲ့အတွက်၊ အခုကမ္ဘာမှာ ကျွန်တော်တို့ရနေတဲ့ နေအလင်းရောင်ရဲ့ ၀.၁% သာရှိမှာဖြစ်တဲ့အတွက် ကျွန်တော်တို့ အသက်ရှင်ဖို့ မဖြစ်နိုင်ဘူးလို့ ယေဘုယျ ကောက်ချက်ဆွဲနိုင်ပါတယ်။

 

လက်ဆွဲနှုတ်ဆက်ခြင်းနှင့်  မှော်ဝင်နှင်းဆီ (Mystic Rose)

            ဆိုပါစို့...။ ကမ္ဘာ့ကုလသမဂ္ဂအထွေထွေညီလာခံကြီးမှာ နိုင်ငံခေါင်းဆောင်ပေါင်း ၁၀၀ တက်ကြမယ်။ သင်ဟာ ကမ္ဘာ့အကြီးဆုံး သတင်းဌာနကြီးတစ်ခုရဲ့ ဓါတ်ပုံသတင်းထောင်တစ်ဦး။ သင့်ကိုပေးထားတဲ့ တာဝန်က နိုင်ငံခေါင်းဆောင်တွေအားလုံးပါတဲ့ လက်ဆွဲနှုတ်ဆက်နေတဲ့ပုံတွေကို ရနိုင်သလောက် အများဆုံးရအောင် ရိုက်ရမယ်။ ရတဲ့အချိန်က တစ်နာရီအတိ။ အဲ့ဒီလိုအခါမျိုးမှာ ဘယ်လို ဗျူဟာမျိုးနဲ့ ဓါတ်ပုံရိုက်ရမလဲဆိုတာကို စဉ်းစားကြည့်ပါမယ်။

            တကယ်တော့ ဒီပြဿနာဟာ သင်္ချာပညာရှင်တွေ စိတ်ဝင်တစား တွေးခေါ်လေ့လာကြတဲ့ လက်ဆွဲနှုတ်ဆက်ခြင်းဆိုင်ရာ ပြဿနာနဲ့ ဆက်စပ်နေပါတယ်။ အဲ့တာက ဒီလိုပါ။ လက်ဆွဲနှုတ်ဆက်ရာမှာ-

အေ နဲ့ ဘီ နှစ်ရောက်ရှိရင် လက်ဆွဲနှုတ်ဆက်မှုတစ်ကြိမ်။

တကယ်လို့ စီ ရောက်လာရင်၊ စီက အေကိုတစ်ကြိမ်  ဘီကိုတစ်ကြိမ် စုစုပေါင်း ၂-ကြိမ်။

တကယ်လို့ ဒီ ထပ်ရောက်လာရင် ဒီက အေ၊ ဘီ နဲ့ စီ သုံးရောက်ကို လက်ဆွဲနှုတ်ဆက်ရမှာမို့ စုစုပေါင်း ၃-ကြိမ်။

အီး ရောက်လာရင်  လက်ဆွဲနှုတ်ဆက်မှု စုစုပေါင်း ၄-ကြိမ် လုပ်ရမယ်။ စသည်ဖြင့် စဉ်းစားသွားနိုင်ပါတယ်။

            ဒါကြောင့်  လက်ဆွဲနှုတ်ဆက်မဲ့လူ ၁၀၀ ရှိရင်၊ လူအားလုံးရဲ့ စုစုပေါင်း လက်ဆွဲနှုတ်ဆက်မှု အကြိမ်အရေအတွက်ကို ရှာမယ်ဆိုရင် 1+ 2+ 3+ 4+...+ ၉၉ ကိန်းစဉ်တန်းရဲ့ ပေါင်းခြင်းကို ရှာရမှာဖြစ်ပါတယ်။ သင်္ချာပုံစံနဲ့ ရေးမယ်ဆိုရင်

            Total sum from 1 to n = 1/2 . r . (r + 1) ဖြစ်ပါတယ်။

            ဒီပုံသေနည်းဟာ ၁၇၀၀ ခုနှစ် နှောင်းပိုင်းမှာ ဂျာမန် သင်္ချာပညာရှင်ကြီး ကားလ်ဂေါက်စ် လူငယ်ဘဝက လေ့လာတွေ့ရှိခဲ့တဲ့ ပုံသေနည်းဖြစ်ပါတယ်။

ဒါကြောင့် လူပေါင်း n အတွက်ဆိုရင်  r နေရာမှာ (n - 1) ကို အစားသွင်းလိုက်ရင်

 

          = 4,950 handshakes ဖြစ်ပါတယ်။

            ဓါတ်ပုံတစ်ပုံရိုက်ချိန်ဟာ ၁၀ စက္ကန့်ဆိုရင် စုစုပေါင်း ၄၉,၀၀၀ စက္ကန့်၊ ၁၃ နာရီ နဲ့ ၄၅ မိနစ် ကြာပါမယ်။ ဒါကြောင့် အားလုံးသော လက်ဆွဲနှုတ်ဆက်မှုတွေကို ဓါတ်ပုံရိုက်ဖို့မဖြစ်နိုင်ဘူး။ ဒါကြောင့် အကောင်းဆုံး အထိရောက်ဆုံးနဲ့ အများဆုံးရနိုင်မဲ့ နည်းလမ်းကတော့ နိုင်ငံခေါင်းဆောင် စုစုပေါင်း ၁၀၀ လုံးရဲ့ ပုံပါအောင် လက်ဆွဲနှုတ်ဆက်မှုပေါင်း ၅၀ ရိုက်မယ်။ အဲ့ဒါက ၅၀၀ စက္ကန့်ကြာမယ်။ သူရတဲ့အချိန် တစ်နာရီ (၃၆၀၀ စက္ကန့်) ထဲက နှုတ်လိုက်ရင်၊ ၃၁၀၀ စက္ကန့်ကျန်မယ်။ အဲ့ဒီ အချိန်နဲ့ နောက်ထပ် နိုင်ငံ့ခေါင်းဆောင် ဘယ်နှရောက်ရဲ့ လက်ဆွဲနှုတ်ဆက်တဲ့ ပုံတွေရိုက်နိုင်မလဲဆိုတာကို တွက်ကြည့်ရပါမယ်။

 

Time t = 10 h

t = 1/2 (n-1) n x 10

t = 5 (n-1)n

3100 = 5 (n-1)n

620 = n² - n

quadratic formula မှာ ထည့်ရှင်းလိုက်မယ်ဆိုရင်

 

            n တန်ဘိုး ၂၅.၄ ရပါတယ်။ ဆိုလိုတာက နောက်ထပ် နိုင်ငံခေါင်းဆောင်ပေါင်း ၂၅ ရောက် ရဲ့ လက်ဆွဲနှုတ်ဆက်နေတဲ့ပုံတွေကို ရိုက်မယ်ဆိုရင် ၅ . ၂၄ . ၂၅ = ၃၀၀၀ စက္ကန့် ကုန်ပါမယ်။ ပိုနေတဲ့ ၁၀၀ စက္ကန့်ကို ကြားလာလ နားချိန်ပဲဖြစ်ဖြစ်၊ တခြားကြုံရာကျပန်း ၁၀ ပုံရိုက်တာပဲပဲဖြစ်ဖြစ် အသုံးချနိုင်ပါတယ်။

            ဒီလက်ဆွဲနှုတ်ဆက်ခြင်းပြဿနာမှာ နောက်ဆက်တွဲ စိတ်ဝင်စားစရာကောင်းတဲ့အချက်ရှိပါတယ်။ အဲ့တာကတော့ နိုင်ငံခေါင်းဆောင်တွေရဲ့ အရေအတွက်နဲ့ သူတို့အချင်းချင်း လက်ဆွဲနှုတ်ဆက်ကြတဲ့ ဖြစ်စဉ်ကို ပုံနဲ့ရေးဆွဲဖေါ်ပြတဲ့အခါ ဖြစ်ပေါ်လာတဲ့ အနေအထားပါ။ စက်ဝိုင်းတစ်ခုရဲ့ ပတ်လည်အနားတစ်လျောက်မှာ နိုင်ငံ့ခေါင်းဆောင်တွေကို နေရာချပြီး၊ လက်ဆွဲနှုတ်ဆက်မှုကို ကိုယ်စားပြုတဲ့ မျဉ်းဖြောင့်တွေနဲ့ အချင်းချင်းဆက်သွယ်လိုက်တဲ့အခါ ရှုပ်ထွေးပြီး စနစ်တကျ ပုံစံကျလှပတဲ့ ပုံတစ်ပုံပေါ်ပေါက်လာပါတယ်။ အဲ့ဒီပုံကို မှော်ဝင်နှင်းဆီ (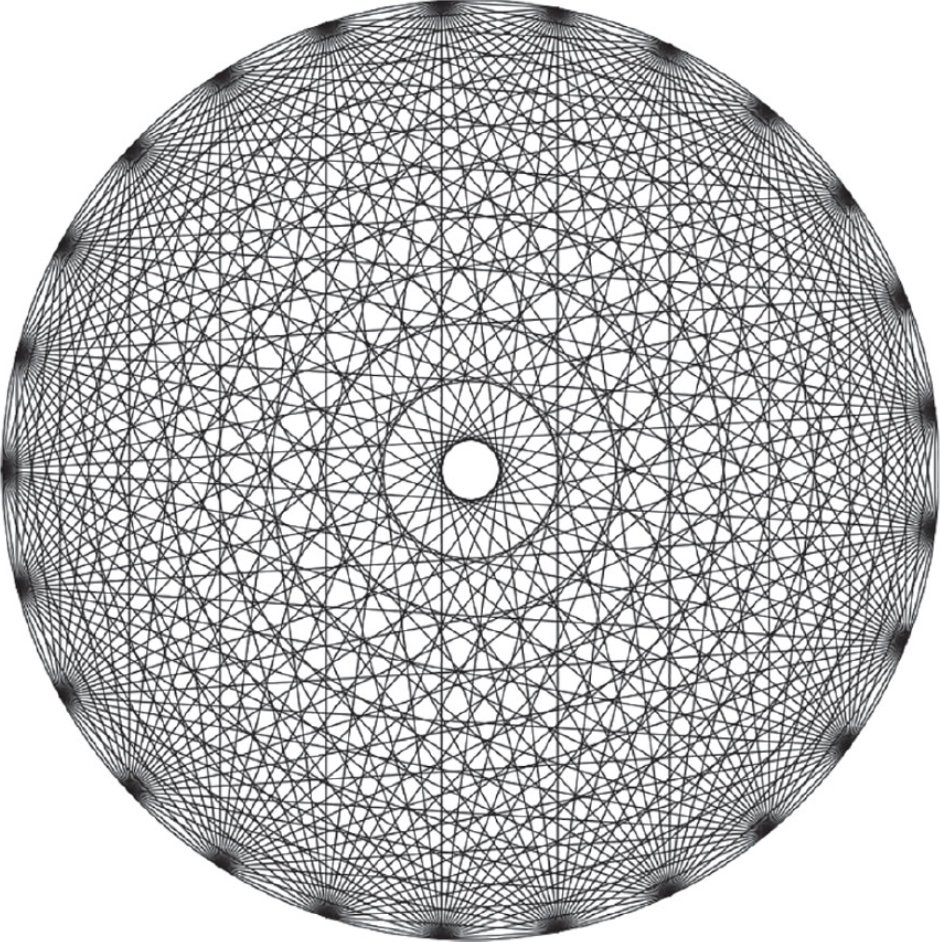Mystic Rose) လို့ ခေါ်ပါတယ်။ အောက်ပါပုံကတော့ နိုင်ငံခေါင်းဆောင် ၁၃ ဦးနဲ့ သူတို့အချင်းချင်းရဲ့ လက်ဆွဲနှုတ်ဆက်မှုကို ဖေါ်ပြထားတဲ့ ပုံဖြစ်ပြီး နောက် တပုံကတော့ နိုင်ငံခေါင်းဆောင် ၂၅ ဦးကို ကိုယ်စားပြတဲ့ပုံဖြစ်ပါတယ်။

N = 13

 

N = 25

 

ကူးစက်ပျံ့နှံ့နိုင်မှုနှင့် အချိန်

            ကောလဟာလ တစ်ခုရဲ့ ပျံ့နှံ့နိုင်မှုနဲ့ပတ်သက်ပြီး စဉ်းစားကြည့်ပါစို့။ ဥပမာ လူတစ်ရောက်ဟာ တစ်နာရီတိုင်းမှာ သူကြားခဲ့တဲ့ ကောလဟာလကို တခြားလူ ၄ ရောက်ကို ဖြန့်နိုင်တယ်ဆိုပါစို့။ အစပိုင်းမှာ တစ်နာရီကို လူဘယ်လောက်အထိ ကောလဟာလ ပြန့်သွားနိုင်မလဲဆိုတာကို တွက်မယ်ဆိုရင်

N = 4 ^t

t က ကောလဟာလပြန့်နှံ့ချိန် နာရီ၊

N က ကောလဟာလကို ကြားရမဲ့ လူစုစုပေါင်းအရေအတွက်။

            အဲ့ဒီ ပုံသေနည်းအတိုင်း၊ ထပ်ကိန်းဖြင့်တိုးတက်မှု (exponential growth)သဘောတရားအရဆိုရင် ၈ နာရီမြောက်တဲ့အချိန်မှာ ကောလဟာလကို နားထောင်ပြီးသူအရေအတွက်ဟာ ၆၅,၅၃၆ ရောက်ရှိရမှာဖြစ်ပါတယ်။

            ဒါပေမဲ့ ပြဿနာက အဲ့လောက်ထိ လူများများကိုပျံ့နှံ့နိုင်စရာမရှိဘူးဆိုပါစို့။ ဥပမာ ကျောင်းသား ၁၀၀၀ ရှိတဲ့ အထက်တန်းကျောင်းတစ်ကျောင်းမှာ "ဒီနေ့ ကျောင်းစောစော ဆင်းလိမ့်မယ်" ဆိုတဲ့ ကောလဟာလမျိုး ပျံ့နှံ့တဲ့ဖြစ်ရပ်ကို စဉ်းစားကြည့်ပါ။ ပထမ ငါးနာရီမှာတင် အဲ့ဒီ ကောလဟာလဟာ ကျောင်းသားပေါင်း (၄ ^၅ = ၁၀၂၄) ပျံ့နှံ့ပြီးခဲ့ပြီဖြစ်နေပါတယ်။ အဲ့ဒီလို ထပ်ကိန်းအတိုင်းသာ တသမတ်တည်း တိုးတက်နေမယ်ဆိုရင်  ပထမ ငါးနာရီအတွင်းမှာပဲ ၊ ရှိသမျှ‌  ကျောင်းသားရေအတွက် ၁၀၀၀ ထက်ကို ကျော်လွန်သွားမှာ ဖြစ်တဲ့အတွက် ( ၄ power t ဟာ) ပြည့်စုံတဲ့    ပုံသေနည်းမဟုတ်ပါဘူး။ ဒါ့အပြင် နောက်ပိုင်း နာရီတွေမှာ အဲ့ဒီကောလဟာလကို ဖြန့်မယ်ဆိုရင် ကြားရတဲ့သူဟာ ကြားဖူးပြီးသားလူ ဖြစ်နေနိုင်ပါတယ်။ ဒါကြောင့် နောက်ပိုင်း နာရီ (အချိန်) တွေမှာ အဲ့ဒီကောလဟာလရဲ့ ပျံ့နှံ့မှုနှုန်းဟာ ကျဆင်းလာရမှာဖြစ်ပါတယ်။ နောက်ပိုင်းကျလာလေလေ၊ အဲ့ဒီ ကောလဟာလကို မကြားဖူးတဲ့လူနည်းပါးလေလေဖြစ်လာမှာပါ။ အဲ့ဒါကြောင့် ပြင်ပလောကနဲ့ အမှန်တကယ်နီးစပ်တဲ့ ကောလဟာလပြန့်နှံ့တဲ့ပုံစံ (logistic equation that models the spread of this rumor) ဟာ

N = 1/  [(1 / 1000) + 0.25^t ]

            ဖြစ်ပါမယ်။ ဒီ သင်္ချာပုံစံအရဆိုရင် ပထမ ငါးနာရီမြောက်မှာ ကျောင်းသားထု တစ်ဝက်ဆီကို လောလဟာလ ပျံ့နှံ့နေပြီးဖြစ်တယ်ဆိုတာ အောက်ပါအတိုင်း တွေ့ရမှာဖြစ်ပါတယ်။

ကျောင်းသား   ၁၀၀၀ အတွက်၊  ၅, ၆, ၇  နာရီ အတွက်

1/  [(1 / 1000) + 0.25^5] = 505.928853755

1/  [(1 / 1000) + 0.25^6] = 803.767660911

1/  [(1 / 1000) + 0.25^၇] = 942.475839853

           

            ကိုဗစ်-19 ရောဂါပျံ့နှံ့ပုံကလည်း ဒီသဘောတရားအတိုင်း ထပ်တူပါပဲ။ လောလဟာလ ပျံ့နှံ့မှုသဘောတရားအတိုင်းပဲ၊ ကိုဗစ် ကူးစက်ပျံ့နှံ့မှုနဲ့ပတ်သက်ပြီး ပြင်ပလက်တွေ့လောကမှာ သုံးတဲ့ SIR Model (S=Susceptible, I=Infected, R=Recovered)မှာလည်း ဒီလိုပဲ အချိန်ကာလအပေါ်မူတည်ပြီး ကူးစက်ပျံ့နှံ့မှုနှုန်းကို ကန့်သတ်ရမယ်ဆိုရဲ့ သဘောတရားကို လိုက်နာပါတယ်။ ရောဂါကူးစက်မှုဟာ အစောပိုင်းကာလတွေမှာ ထပ်ကိန်းနှုန်းနဲ့ တရှိန်ထိုးကူးစက်ပေမဲ့ နောက်ပိုင်းအချိန်တွေမှာ အသစ်ထပ်မံ ကူးစက်ခံရမဲ့လူအရေအတွက်ဟာ တဖြည်းဖြည်း နဲပါးသွားတဲ့အတွက် ကူးစက်မှုနှုန်းဟာ တဖန်ပြန်လည် ကျဆင်းလာရမှာဖြစ်ပါတယ်။

           

            နိဂုံးချုပ်အနေနဲ့တင်ပြလိုတာကတော့ ဘယ်လို ဘယ်လောက်ပဲ ရိုးရှင်းတဲ့ သင်္ချာလုပ်ထုံးပဲဖြစ်ဖြစ်၊ လူတိုင်းနားလည်ပြီးသား လွယ်ကူတဲ့ ပုံသေနည်းလေးပဲဖြစ်ဖြစ်၊ ကျွန်တော်တို့ တတွေရဲ့ နေ့စဉ်ဘဝ တွေးခေါ်လုပ်ကိုင်ဆောင်ရွက်မှု တွေထဲမှာ နက်နက်ရှိုင်းရှိုင်း ကျယ်ကျယ်ပြန့်ပြန့် နေရာယူပြီးသားဖြစ်တဲ့အတွက် အကျိုးရှိအောင် ပြန်လည်ဖော်ထုတ် လို့ရတယ်ဆိုတဲ့အချက်ပဲဖြစ်ပါတယ်။ ရိုးရှင်းတဲ့သင်္ချာသဘောတရားလေးတွေကို အသုံးချပြီး ခန်းနားတဲ့ အတွေးစိတ်ကူးတွေ ဖန်တီးတည်ဆောက်နိုင်ပါစေ။

                                                                                                                        

Note:    ၂၀၂၁ "ဆွေခိုင်ဆု" သင်္ချာစာပေပြိုင်ပွဲ ဆုရဆောင်းပါး

copyright©ဆွေခိုင်ဆု